その思考実験を更に深堀すると、ハイゼンベルクの不確定性原理から導かれる、「1つの電子が同時に2つのスリットを通り抜けて、それらが干渉模様を作る」 それは量子力学の都市伝説ですが、その量子力学の都市伝説を否定する結果が得れました。
もう一つの大きな発見は光のエネルギの算出にプランク定数を使う方法の限界が分かりました。
実験の概要
単発の電子を2重スリットに向けて1発づつ発射する。それを繰り返す。もし電子が粒子性だけを持つのであれば、電子は直線的に飛行する。 その結果スリットの背後にあるスクリーンには均一は模様ができる。
回析模様は2つの波が作る模様ではありません。一つの波で作られます。
それは、スリットを通り抜けた後に波の回りこみで生まれます。 その回りこみの距離の違いで回析模様が生まれます。
方形パルスのL->H(立ち上がり)、H->L(立下り)の時間はほぼゼロの方形パルスを想定します。 パルス状態は常にHかLの2値だけを示すパルスです。
方形パルスの高さHはスリットの幅Dより十分に小さいので方形パルス全体がスリットを通り抜けかけます。
その時にスクリーンに現れる回析模様は方形パルスLとHの位置、すなわちパルスの高さの2本の線となります。
1.電子の飛行を弾丸モデルを使うと、回析模様が実験の精度によって生まれます。 1つのスリットを1つの電子が通り抜けるだけ回析模様ができます。
実際は、電子の飛行が波動性を持つのでスクリーンには回析模様ができる。
実際の実験で観測されています。
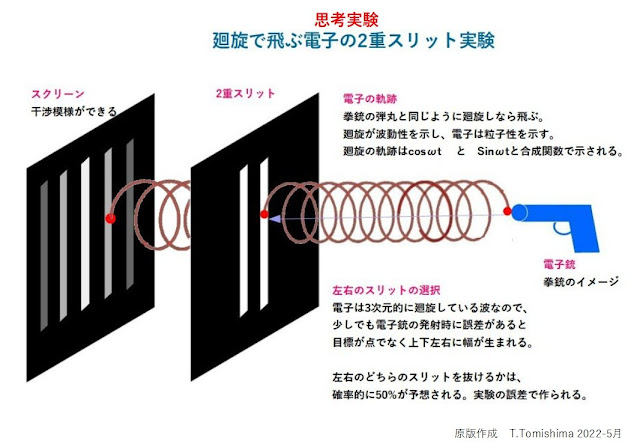 |
| Fig.1 電子の2重スリット実験の光子の弾丸モデル |
どうして回析模様ができるか
従来の考え
多くの人の光と電磁波の飛行が波動性を持つ姿の連想は海の波のような物です。真空中には媒質がないので、光や電磁波の飛行が海の波のような姿は成立しません。しかし多くの人の頭のあるイメージは海の波の姿に固定されたままです。
植木ひとしさんの「分かっているけど止めらない」という事です。相田みつおさん「人間だもん」でもいいです。 その波イメージで実験結果を検討するのが習い性になっています。それでいろいろと結果の理解に無理が生まれています。
ここでは電子が2つのスリットを通り背後のスクリーンにできるのは干渉模様です。 干渉模様は2つも波の粗密による打ち消し合って弱まる、更には消えるか、あるいは強み合うことで強調されるかでできる模様です。
干渉模様を作るには2つの波が必要です。 それで一つの電子を発射したにもかかわらず、同時に2つのスリットを通り抜けて干渉し合って干渉模様ができたとこれまでは考えてられていました。
別の言葉で言うと干渉模様ができたことは2つのスリットを同時に通り抜けた2つの波がある証であると考えてられていました。
海の波のモデルが頭にあるとどうしてそのような考えに陥ってしまいます。それで幻が現実のように語られていました。
弾丸モデルでは
弾丸モデルでできるのは、一見すると干渉模様と同じように見えますが、干渉模様でなく回析模様です。回析模様は2つの波が作る模様ではありません。一つの波で作られます。
それは、スリットを通り抜けた後に波の回りこみで生まれます。 その回りこみの距離の違いで回析模様が生まれます。
回析模様を詳しく説明
弾丸モデルは3次元の立体モデルです。 Sin波とCos波の合成関数です。電子が粒子性だけの場合
2次元でも3次元でも同じ結果になります。
下図Fig.2の上の例が電子が粒子性だけの場合です。
電子は直線的に飛びスリットを通し抜けてスクリーンと到達します。
そのスクリーン上には1点だけの跡が残ります。
2次元モデルのSin波
3次元の立体モデルは複雑なので、2次元の単純なモデルで考えます。
平面上にSin波が一つでスリットも1つです。
下図Fig.2の下の例です。
電子の発射装置が完全理想状態であれば、毎回理想的に位相と方向性が同じになります。
その時はスリットを通過する点が1点になります。
A点だけです。回析模様はできません。
電子の発射装置の位相と方向性に誤差
しかし現実の電子の発射装置は位相と方向性に誤差があります。
下図Fig.2の下の例は発射時に位相の誤差が生じた場合にはB点でもスリットを通り抜けます。
これが発射時に位相の誤差により生まれる回析模様になります。
1つのスリットでA’とB’の2本の線がスクリーン上に現れます。
スリットが2本であれば4本になります。
立体の弾丸モデルでの回析模様の線の数
また現実の姿に近いの3次元の立体の弾丸モデルを考えます。
それはSin波とCos波の合成関数なのでスクリーン上に現れる線は2次元モデルの2倍になります。 1つのスリットで4本の線。 2つのスリットで8本の線になります。
 |
| Fig.2 2次元の弾丸モデルの回析模様 |
台形パルスで位相のずれを検討
位相のズレで回析模様ができることを台形パルスを使うと理解し易いです。
下図Fig.3は2つの台形パルスが書かれています。 両者に位相差があります。
スクリーンには位相のズレにより台形パルスの振幅の幅で回析模様が2本できます。
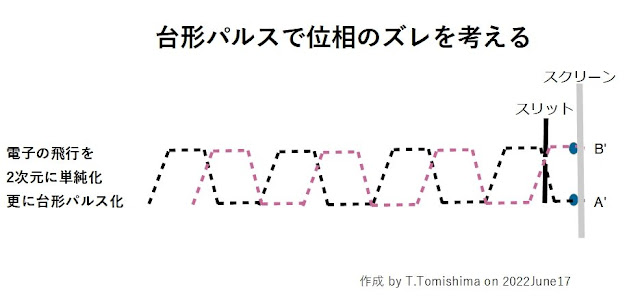 |
| Fig.3 台形パルスで電子の飛行を位相のずれを検討 |
方形パルスで回析模様を検討
方形パルスで回析模様を更に思考実験をします。Fig.4に示してあります。
方形パルスの高さはスリットの幅Dよりも小さいです。
方形パルスのL->H(立ち上がり)、H->L(立下り)の時間はほぼゼロの方形パルスを想定します。 パルス状態は常にHかLの2値だけを示すパルスです。
方形パルスの高さHはスリットの幅Dより十分に小さいので方形パルス全体がスリットを通り抜けかけます。
その時にスクリーンに現れる回析模様は方形パルスLとHの位置、すなわちパルスの高さの2本の線となります。
重要な2点が分かる
全てわかって言っている訳ではありませんが、実は本当に重要が事が方形パルスの回析模様の思考実験で分かりました。
現実の電子の2重スリット実験で回析模様が観測されたら、
1)回析模様の間隔の長さが入力された波形の振幅を示している。
2)量子力学の世界では光子の振幅はプランク定数の幅で正規化されているが、おそらく予測される回析模様の幅はプランク定数長1.6*10の-34乗よりも十分に大きな数値になる。
何が言いたいかというと、正規化された光子の振幅では自然界の本当の姿を語るには十分でない。
光子の振幅はプランク定数の幅で正規化されている
いったい何といっているのが多くの人は理解できないと思います。
この光子の振幅の正規化については別ブログ記事で説明します。
 |
| Fig.4 波長のL/H比が極端に大きいパルスの回析模様 |
今回の思考実験で分かったこと
たびたびになりますが、全てわかって言っている訳ではありません。 従来の量子力学の定説を覆す結論になりました。半信半疑ですが、多分間違いないと考えています。
1.電子の飛行を弾丸モデルを使うと、回析模様が実験の精度によって生まれます。 1つのスリットを1つの電子が通り抜けるだけ回析模様ができます。
従来の量子力学の定説:
干渉模様ができるのは1つの電子が同時に2つのスリットを通り抜ける。 その2つの波の干渉でできる。 これはハイゼンベルクの不確定性原理を示している。
今回の思考実験の中ではそんな事実はでてきません。1つが同時に2つ存在する話やトランスポーテーションなどの量子力学の都市伝説はどうやらありません。
2.光のエネルギーを考えるには 正規化されたプランク定数の振幅だけで不十分である。
以上
コンテンツは全てオリジナルです。引用は明記しています。
著作権保護に配慮をお願いします。
Copyright © 2021 光速100万km/s 冨嶋 努





0 件のコメント:
コメントを投稿