芭蕉の有名な俳句「古池や蛙飛びこむ水の音」から発想を得てドップラー効果を思考実験をしました。すると従来のドップラー効果の理論を拡張する新しい理論が生まれました。
今回は思考実験で生まれた新しいドップラー効果の理論の基本的な考え方を紹介します。
記事の連載回数
最初考えていたドップラー効果の記事は1回で終える予定でした。 しかし次々と湧き出る疑問を突き詰めていると記事が膨らんでしまいました。 頭の中ではあらすじがほぼ完成しています。 あとは詳細を詰めながら活字にします。
記事内容は「芭蕉の俳句とドップラー効果」、「音のドップラー効果」、「光のドップラー効果」、「2重衛星のドップラー効果」、「従来のドップラー効果の理論の課題」等の考察が広がりました。 それで全体とし3回程度の連続記事を予定しています。
ドップラー効果の思考実験の背景
どうしてドップラー効果の思考実験をしようと思ったかというと、光速の可変性を証明する為です。
アインシュタインの特殊相対性理論の根底にある理論は、光速の不変性であり、光の発生源の速度の影響を受けないという点です。
そのアインシュタインの特殊相対性理論を支えるのが、ド・シッターの2重衛星に関わる実験です。 天文学的な観察から光速の不変性があり、光の発生源の速度の影響を受けないが結論つけられています。*1)
ド・シッターは2重衛星の関する5つの論文を書きました。*1) 私はその5つの論文の内の3つを読みました。 2つの論文はネットを探しても見つけることができませんでした。
その論文の反証を考えていましたがそれは止めました。 代わりに光のドップラー効果の新解釈を反証に使う事にしました。
その方がより分かり分かり易く、賛同も得やすいと考えました。
それでドップラー効果の思考実験になりました。
松尾 芭蕉の俳句
古池や 蛙飛びこむ 水の音
Donald Keene、ドナルド・キーンさんの英語訳では
The ancient pond
A frog leaps in
The sound of the water.
この芭蕉の俳句と走る列車の組み合わせでドプラー効果を思考実験します。
ドップラー効果の思考実験の条件
速度Vt で走行している列車の中に丸いたらいがあります。
たらいを古池と考えて頂いてもいいです。
列車外に静止した観測者がいます。
線路から1m離れた位置に立っています。
そのたらいに蛙が飛び込みます。
そして波紋と音が生まれます。
そのたらいに出来た波紋が観測者にどのように見えるかと、
飛び込みの音が観測者にどのように聞こえるかの思考実験です。
たらいの波紋
蛙がたらいに飛び込みむとたらいの水面に波が生まれます。
そして波紋ができます。
それは速度Vwで広がっていきます。
列車外の観察者から見た波紋の速度
波紋の速度は早くなっているように見えるはずです。
列車の速度が加算されたように
観察者から見た波紋の速度 = Vw + Vt
もう一つ重要な点は列車上の波紋の速度は変化がありません。
Vwのままです。
更に注意して欲しいことは、1匹の蛙の飛び込みで出た波なので単発の応答です。
連続して次々を新たな波が生まれている訳ではありません。
光で例えると、光の連続発光のような物でなく、光子を1発だけ発射したものです。
 |
| 芭蕉の俳句でドプラー効果を思考実験 Fig.1 古池や蛙飛びこむ水の音 *1) |
蛙と観察者が静止しているドプラー効果がない時
蛙が飛び込んだ時の音よりも音階のA(ラ),B(シ),C(ド)の単音を歌う方が分かり易いので変えました。
A(ラ)は440Hzのサイン波です。
B(シ)は493.8Hzのサイン波です。
C(ド)は523.2Hzのサイン波です。
Fig.2です。蛙が歌います。 A,B,Cの単音をそれぞれ1秒間発声します。
それを少し離れたところにいる観察者が聞きます。
観察者は離れているので音の到着は少し遅れますが、
同じように1秒間隔でABCと音を聞きます。
周波数に変化はありません。 同じ音を聞きます。
蛙と観察者の時間は同じように流れます。
平行線的に音が到達しているイメージです。
音のドップラー効果をシンプルに説明
蛙が移動して観察者が静止している
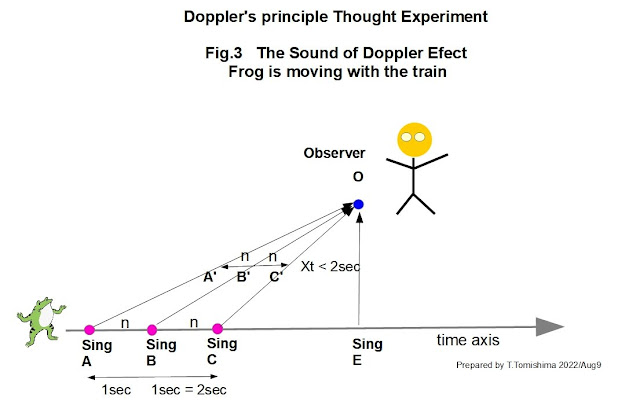
Fig.3です。 蛙が電車に乗って速度Vtで移動しています。
そして1秒間隔でA,B,Cを歌います。
それぞれ1秒間発声を続けます。
観察者が停止していて蛙が移動しているので、音が観察者まで飛ぶ距離はだんだん短くなります。 A-O,B-O,C-Oを見て下さい。 長さが短くなっていることが分かります。
早く音が聞こえる
この音の飛ぶ距離が短くなる意味は、音が早く観察者に到着します。
すると観察者はAが聞こえてからCが聞こえるまでの時間が少し早くなります。
波の数n、周波数f
Fig.3中に「n」とあるのが、波頭の数です。Aはラの音なので440Hz のサイン波が1秒間続きます。 nが440個あることになります。 周波数のfと同じ事です。
蛙と観察者の間の示してある横線A’、B’、C’の間隔が観察者の聞こえる時間の間隔になります。
確かに間隔は短くなりましたが、その中身の「n」の数に変わりはありません。
それで周期の時間が短くなってnが同じなので周波数が高くなることが分かります。
これが音のドップラー効果です。
横線A’、B’、C’の間隔は厳密なものでありません。
周波数が変わることを直観的に伝える為のイメージです。
飛行する距離が変化すると周波数が変わる
これから分かることは音のドップラー効果とは音波の到着時間、即ち飛行する距離が変化することが周波数を変化させています。
飛行する距離が連続的に変化しないとドップラー効果は生まれません。 それは単に音の発生源と観察者が静止しているだけです。
もうひとつの重要な点があります。 観察者のO点と横並びになった時のE点の音の周波数は蛙は発した原音が観察者に聞えます。
そして観察者Oを通り過ぎると今までと真逆のこと起きます。
今度は聞こえる周波数が低くなっていきます。
観察者Oを軸に対象性があります。
従来のドップラー効果の同一軸のモデル
Fig.3の観察者OをEに重なると従来のドップラー効果の同一軸のモデルです。速度でドップラー効果を捉えていますが、実は距離の変化が重要です。
まとめ
ドップラー効果とはをできるだけシンプルに説明すると、
音のドップラー効果とは音波の飛行する距離が連続的に変化することが周波数を変化させています。
距離が変化するとは音源と観察者の相対的距離の変化になります。
そして観察者に最接近した時に音源の原音になります。
更に観察者Oを軸にしてドップラー効果は対象性があります。
次回の記事
次回の記事では音のドプラー効果をより詳しく説明します。
数式で音のドプラー効果を表現します。
そして従来のドプラー効果の理論の違いを明確に示します。
音のドップラー効果の新理論では、光のドップラー効果もその新理論で説明ができます。
すると光の可動性も説明ができます。 ド・シッターの2重衛星の実験結果の反証になります。
資料
1a) ド・シッター de Sitter, W., (1913):
"A Proof of the constancy of the velocity of light";
光速が一定であることの証拠
https://en.wikisource.org/wiki/A_proof_of_the_constancy_of_the_velocity_of_light
1b)ド・シッターの4つの論文
"An Astronomical Proof for the Constancy of the Speed of Light";
A Proof of the constancy of the velocity of light"
https://en.wikisource.org/wiki/A_proof_of_the_constancy_of_the_velocity_of_light
1c) "the independence of the speed of light from the movement of the source"; de Sitter, W.
光速が光源の動きから独立している
1d) "On the constancy of the velocity of light". de Sitter, W.
光速の一定について
1e) " Doppler's principle and the ballistic theory of light" de Sitter, W.
ドップラーの原理と光の弾性理論
Bulletin of the Astronomical Institutes of the Netherlands, 2, 163. ISSN 0365-8910.
https://www.narcis.nl/publication/RecordID/oai%3Ascholarlypublications.universiteitleiden.nl%3Aitem_2718704/uquery/Doppler%27s%20principle%20and%20the%20ballistic%20theory%20of%20light/id/1/Language/EN1924
2)Fig.1中の蛙のイラストはダ鳥獣ギ画さんの画像です。
https://chojugiga.com/2017/09/05/da4choju53_0023/
3) ドップラー効果の説明 Wiki
波(音波や電磁波など)の発生源(音源・光源など)と観測者との相対的な速度の存在によって、波の周波数が異なって観測される現象をいう。
https://ja.wikipedia.org/wiki/%E3%83%89%E3%83%83%E3%83%97%E3%83%A9%E3%83%BC%E5%8A%B9%E6%9E%9C
Copyright © 2021 光速100万km/s TsutomuTomishima





0 件のコメント:
コメントを投稿