ドップラー効果の思考実験で生まれた新しいドップラー効果の理論を詳しく説明します。
今回の記事では音のドップラ効果の新理論の数式を作りました。
そして従来のドップラー効果の数式と比較します。
従来のドップラー効果の数式では実際に観測される現象を説明するには不足している点があります。それをこの記事で説明します。
ドップラー効果の新理論
できるだけシンプルに説明すると、
音のドップラー効果とは音波の飛行する距離が連続的に変化すると周波数が変化する
距離が変化するとは音源と観察者の相対的距離の変化になります。
そして観察者に最接近した時は音源の原音になります。
周波数の変化はありません。
更に観察者Oを軸にしてドップラー効果は対象性あります。
上記の内容がFig.1に示されています。
前回の記事内容
前回の記事でドップラー効果の新理論の概要を分かり易く説明しています。
新理論の概要を知りたいときは以下のブログ内容を読んで下さい。
ドップラ効果の新理論の数式表現
Fig.1 ドップラ効果の新理論の概念図は2次元的に表現されています。光のドップラー効果でいう横ドップラーに相当します。
それを数式表現するには音源の移動速度の成分の距離での調整があります。
その他に音源と観察者の位置関係を2次元的の表現も必要になります。
ドップラ効果の新理論の1次元表現
Fig.1の横ドップラーで観察者と音源の両方が移動する場合は、数式がちょっとだけ複雑になります。
それで新理論をシンプルに数式で分かってもらう為に1次元の線上で表します。
Fig.2になります。
従来の一般的なドップラーの数式が想定しているモデルです。
光の場合の縦ドップラーと呼ばれています。
観察者が音源がお互いに離れていきます。
観察者が観測される音は周波数が低くなります。
Fig.2の上側の図です。
観察者が音源がお互いに近づいていくのは Fig.2の下側の図です。
観察者が観測される音は周波数が高くなります。
OとAが重なった時は音源のオリジナルの周波数になります。周波数の変化はありません。
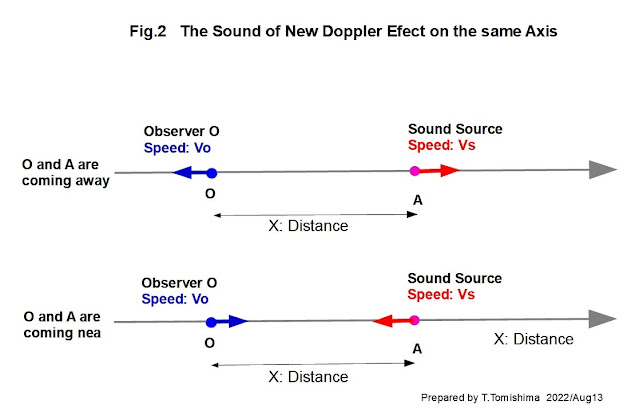 |
| Fig.2 ドップラ効果の新理論の1次元表現 |
ドップラ効果の新理論の数式の考え方
音のドップラー効果は音源と観察者の相対的距離の連続的な変化になります
相対的距離がゼロの時は音源の周波数になります。 周波数の変化はありません。相対的距離の連続的な変化は音源と観察者の速度で決められます。
時間経過で相対的距離は変化します。
それで数式には時間の要素が数式に入れる必要があります。
周波数の変化の割合は、音源と観察者の速度を音速で割った比率で求められます。
数式を求める
観察者が音源がお互いに離れていく
観測される音の周波数が低くなる場合です。
Fig.2の上側の図を数式にすると
f' = f0 + (f0の減少分)
ここでf0の減少分とは、音波が飛行する距離の変化です。
f' = f0 - f0 *( Vo + Vs)/S )*t
式(1)
f': ドップラ効果の音(観測される周波数)
f0: 原音の周波数
S: 音速 m/sec
Vo: 観察者が離れていく速度 m/sec
Vs: 音源が離れていく速度 m/sec
t: OとAが重なった時点をゼロとして、そこから離れていく時間
観察者が音源がお互いに近づいていく
Fig.2の下側の図を数式を同様に求めると
周波数の変化分がプラスされただけです。
f' = f0 + f0 *( Vo + Vs) / S )*t
式(2)
f': ドップラ効果の音(観測される周波数)
f0: 原音の周波数
S: 音速 m/sec
Vo: 観察者が近づいていく速度 m/sec
Vs: 音源が近づいていく速度 m/sec
t: OとAが重なった時点から逆算した時間
従来のドップラ効果の理論の数式
wikiで示されているドップラ効果の数式の条件です。観測者も音源も同一直線上を動き、音源S (Source) から観測者O (Observer) に向かう向きを正とすると、観測者に聞こえる音波の振動数は、*1)
上記の引用の条件は新理論の式(2)の条件と同じです。
wikiでの従来のドップラ効果の数式は
(他のネット情報でも同じ数式です*2))
2)Doppler Effect
f' = f0 * ( S - Vo ) / ( S - Vs ) 式(3)
対して新理論の式は
f' = f0 + f0 *( Vo + Vs ) / S )*t 式(2)
微妙に違っています。
例えば定数項としての従来のドップラ効果の数式にはF0がありません。
更に時間の増減の要素のtがありません。
従来のドップラ効果の数式の課題
1)観測される音源の周波数が連続的変化する概念が含まれていない。
時間の要素が式に入っていない。
2)本当は観測者と音源が重なった時、両者の距離がゼロになっと時です、音源の原音の周波数が観測されます。 その原音の周波数があることが従来のドップラ効果の式では見えてきません。
3)音源が観測者に接近して、次に観察者を通り過ぎて時を考えます。
両者が離れていく場合です。
その時には
本当はドップラ効果に対象性があります。 周波数の変化が同じようになります。
それが従来のドップラ効果の数式では見えて来ません。
まとめ
ドップラ効果の新理論の数式はシンプルです。
観測者と音源が近づく場合は観測される周波数は増加するので、下記の「+-」はプラスになります。
観測者と音源が離れて行く場合は周波数は増加するので下記の「+-」はマイナスになります。
f' = f0 ✙- f0 *( Vo + Vs )/ S )*t
f': ドップラ効果の音(観測される周波数)
f0: 原音の周波数
S: 音速 m/sec
Vo: 観察者が離れていく速度 m/sec
Vs: 音源が離れていく速度 m/sec
t: OとAが重なった時点をゼロとして、そこから離れていく時間
OとAが重なった時点では原音の周波数がそのまま聞こえることが式に含まれています。
時間の要素が入っているので、連続的な周波数の変化を記述できています。
光のドップラ効果を考える
音のドップラ効果の新理論を見ると、音源の移動速度からドップラ効果を求めています。
音波の速度が距離の変化を作りだして、音波が飛行する時間の変化がドップラー効果です。
言ってみればドップラ効果とは音源から発射される音波の速度で作られています。
音源の速度が音波の速度を変えてます。 それがドップラ効果です。
ドップラ効果とは音源の速度が発射される音波の速度を変えたので生まれたと言えます。
ドップラ効果が確認できたら、飛行する音波の速度が相対的に変化があったということです。
光の場合
光でも同じです。 光のドップラ効果が観測されたら、光速に変化があったことになります。 赤色偏向があれば、光速が秒速30万kmより遅くなったことを意味します。
青色偏向があれば秒速30万kmより早くなったことを意味します。
このくだりは厳密にはもう少し補足説明が必要です。 次の記事で説明する予定です。
次回の記事内容
次回の記事では光のドップラ効果を新理論で詳しく説明します。
資料
1) ドップラー効果の説明 Wiki
波(音波や電磁波など)の発生源(音源・光源など)と観測者との相対的な速度の存在によって、波の周波数が異なって観測される現象をいう。
https://ja.wikipedia.org/wiki/%E3%83%89%E3%83%83%E3%83%97%E3%83%A9%E3%83%BC%E5%8A%B9%E6%9E%9C
https://byjus.com/physics/doppler-effect/
コンテンツは全てオリジナルです。引用は明記しています。
著作権保護に配慮をお願いします。 Copyright © 2021 光速100万km/s TsutomuTomishima





0 件のコメント:
コメントを投稿