量子力学の世界では、空間を瞬間移動したり、1つの存在が同時に二つ存在する事があり得ると言われています。ハイゼルベルグの不確定性原理の拡大解釈です。
拡大解釈の大きな理論の根拠となっているのが電子の2重スリット実験での干渉模様です。 しかし電子の飛行を螺旋モデルで検討すると、拡大解釈の根拠は消えました。そして不確定性原理の拡大解釈はないと結論づけました。
ハイゼルベルグの不確定性原理
慶応大学にあった資料が分かり易いです。*2) その一部を使って説明します。
そして,誤差 ∆x と ∆p は,次の「ハイゼンベルグの不確定性原理」を満たす.すな わち, ∆x · ∆p + ~(= プランク定数/2π+1.5547 × 10−34Js). (4.20)したがって,一方の精度を上げれば,必然的に,他方の精度は落ちる
この式4.20の意味は、ミクロ精度で位置∆x と運動∆pを掛けた関係はアバウト・イコール(~=)でプランク定数/2πになると言ってます。
掛け算の結果が大体それ程度を示す、アバウトな結果だと言っています。
アバウトな結果を作る掛け算なんので、どちらかが一方が無限に小さくなると、もう一方は無限に大きくなります。
数式の解釈次第で、位置と運動の関係性をどうにでもできます。
解釈をする人のさじ加減次第です。それで拡大解釈の余地が大きくなります。
不確定性原理の拡大解釈とは
干渉模様とは
電子の2重スリットの実験ではスクリーンに均一な衝突の跡が予測されました。
しかし実際の衝突の跡は、干渉模様になりました。
干渉模様は2つの波の強弱の重なりで作られます。 2つの波の山と山が重なりると、衝突の跡は強調されます。 反対に波の山と谷が重なると、打消し合って弱い衝突の跡になります。
干渉模様の意味するのは
干渉模様が出来るには同時に2つの波が必要です。
一つの電子を発射したにも関わらず同時に2つの波があったことになります。
その1つの電子が2つのスリットを同時に通り抜けて干渉模様が出来たと解釈されました。
一つの存在が同時に2つ存在する、常識では考えられないようなことが量子のミクロの世界では起こった。 それが厳密な実験の場で明らかになったと理解されました。
実はその解釈は違うのではないかと言うのが本ブログの記事内容です。
唯一の実験結果
私の理解では、「1つの存在が同時に2つの存在になる」が観測されたのは、電子の2重スリットの実験の干渉模様です。
その実験だけです。それ以外にそのような現象は観測されていません。
拡大解釈
1つの存在が2つの存在する超怪奇が現実に起きるなら、その延長上に空間を瞬間移動する事があって確率的に絶対にゼロとは言い切れない、それが起きても不思議でない。 確率的にはそのような事象も考えられると更に拡大解釈されました。
「1つの存在が2つの存在」と「瞬間移動」は量子力学の確率的な側面の拡大解釈です。 厳密には先に説明した「ハイゼンベルグの不確定性原理」とは関係はありません。
しかし「不確定性原理」の不確定性という言葉の響きから、ミクロの世界で不可思議が起こると「ハイゼンベルグの不確定性原理」と言う言葉が広く使われているようです。
追加説明:「不確定性原理の拡大解釈」 2022-July5
リチャート・P・ファインマン先生
アインシュタイン先生の亡き後の物理界のスーパースターはリチャート・P・ファインマン先生でした。1988年に朝永振一郎先生と同時にノーベル物理学賞を受賞されました。
正に物理界の巨人です。実は最近知りました。
そのリチャート・P・ファインマン先生は量子力学のミクロの世界では、一般常識では理解できないような現象が起こると言っています。
例えば、量子力学はミクロの世界を確率で考えるので、可能性が極めて低い現象も排除できません。ハイゼルベルグの不確定性原理です。
それを都合のよいように拡大解釈しました。
分かり易く言うと「何でもあり」です。
ファインマン先生の信じていること
例えば下図Fig.1のように1つ電子を2つのスリットに向けて発射したら。再度強調しますが、1つの電子を発射します。
すると1つの電子が同時に2つのスリットを通り抜けて背後のスクリーンに当たる。
或いは1つの電子が瞬間移動して遠く宇宙の先にあるアンドロメダ銀河への長い旅をして帰ってきて、左のスリットを通ってスクリーンに達する。
それらは確率的にあり得ると主張されています。
 |
| Fig. 1 電子の2重スリット実験で電子が辿る様々な飛行経路 |
書籍ブライアン・グリーン著「エレガントな宇宙より」からの抜粋
ファインマン先生の主張を書籍から抜粋
ファインマン先生の主張です。ブライアン・グリーン著 書籍「エレガントな宇宙より」からの抜粋を下に示します。
燐光スクリーンに届く一つ一つのの電子は実は両方のスリットを通りぬけのだと。ばかげているように聞こえるに違いないが、待っていただきたい。
この先話はもっと滅茶苦茶になるので、
ファインマン先生はこう論じた。
電子線源から燐光スクリーンの1点まで進むとき、じつは個々の電子は通りうる全ての進路を同時に通るのだ。
図4-10に進路をいくつか示した。 電子はすんなりと左のスリットにを通る。同時に右のスリットもすんなりと通る。 左のスロットに向かい、突然、経路を変えて右のスリットを通る。 行きつ戻りつして、最後に左のスリットを通る。アンドロメダ銀河への長い旅をして帰ってきて、左のスリットを通ってスクリーンに達する。 道筋はこのようにいくらでもある。
ファインマン先生と物理界が間違った理由
1つ目は
光子が波動性と粒子性を示します。電子も。 ファインマン先生および物理界はその飛行の姿を明確に示さず、数学的な確率でミクロの電子の経路状態の記述をしています。
確率の数式で描く世界ですので、どんな状態も全否定はできません。
拡大解釈が生まれます。 電子がアンドロメダ銀河に旅してからスリットを通り抜けるとも解釈できます。
メディアも悪いです。電子が瞬間移動してアンドロメダ銀河を旅すると言った方が一般受けします。それに乗っかり続けたようです。
量子力学界はその不確かな土台の上で理論展開をこれまでずっとやって来ました。
常に曖昧さを含む前提条件で理論と実験を進めています。
2つ目は、
電子の2重スリット実験で干渉模様が出来た。 干渉模様が出来るには2つの波が必要です。 1つの電子を発射したのに関わらず、干渉模様に必要な干渉模様が生まれるには1つが同時に2つのスリットを通り抜ける必要があります。
1つの電子が同時に2つ存在することが実験で示された。 ハイゼルベルグの不確定性原理の現れはミクロの世界では真実であると理解した。
信じられない事が実際にあった例として電子の2重スリット実験の結果を理解した。
3つ目は
上の2つ目の理由に関係しているが、スクリーンに現れているのは干渉模様でなく回析模様です。 電子の飛行が螺旋であれば、スクリーンに残る電子の跡の位置の分布の偏りで模様が生まれます。 レーザーの干渉模様も同じです。
下図は電子の飛行が螺旋を描く概念図です。 波動性と粒子性が分かります。
図を見れば感覚的に回析模様が出来そうと理解でします。
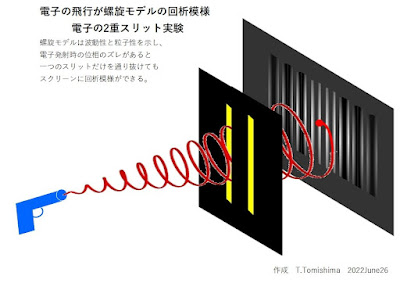 |
| Fig.2 電子の2重スリット実験の螺旋モデルの概念図 |
4つ目は
回析模様は実験時の誤差で生まれます。
電子の発射時の位相のズレ、方向性のズレ、エネルギーのバラツキによる周波数のズレで生まれます。
詳しくは過去のブログ記事で詳細に説明しています。
5つ目は、
これが一番大きいと思いますが、物理界のスパースターのファインマン先生に反旗を翻したり、物理界常識に反すことを言うと、物理界での仕事がなくなります。
物理や量子力学の世界で今後生きて行こう、生計を立てて行こうと考えている研究者に取っては、不確定性原理の拡大解釈は不可触の話題です。
下手な事を言うと露頭に彷徨うことになるので、おかしいと疑問を感じても口に出せません。
物理界の業界人ではありませんが、どこの業界でも同じような事があります。
それで推測ですが多分当たっていると思います。
どこかでまずいと思いつつ変われない現実があります。
その時は新しい風が外から来ます。
ペルーの黒船しかり、
私は好奇心が強いです。それで自分の興味と疑問の解消が第一でやっています。
その私のこのとんでもない仮説が小さい風の一つにでもなれて、役に立てればいいなと願っています。
まとめ
電子の飛行が螺旋の姿を取ると仮定して、実験の誤差を綿密に検討すると、
物理界の巨人ファインマン先生が信じ、物理界で信じられている不確定性原理の拡大解釈。そんなものはありません。まぼろしです。
空間を瞬間移動することもありませんし、1つの存在が同時に二つ存在することもありません。
確率の数式の解釈のトリックと実験の誤差です。
資料
1) 書籍ブライアン・グリーン著 書籍「エレガントな宇宙より」
2) 4.3 ハイゼンベルグの不確定性原理
https://www.math.keio.ac.jp/~ishikawa/KoaraCopen/Copen04_03.pdf
3) 不確定性原理とは(コトバンクから)
https://kotobank.jp/word/%E4%B8%8D%E7%A2%BA%E5%AE%9A%E6%80%A7%E5%8E%9F%E7%90%86-123742
4) 不確定性原理(ゆうこーの大学物理教室)
https://yuukou-potential.com/pre-uncertainty/
コンテンツは全てオリジナルです。引用は明記しています。
著作権保護に配慮をお願いします。 Copyright © 2021 光速100万km/s TsutomuTomishima




0 件のコメント:
コメントを投稿